三角形的三邊關系定理是什么？

答：筆下學習網整理了關于初中數學復習知識點：三角形的三邊關系定理，希望對同學們有所幫助，僅供參考。

三角形三邊關系定理（也稱三角形不等式）

（一）定理內容：

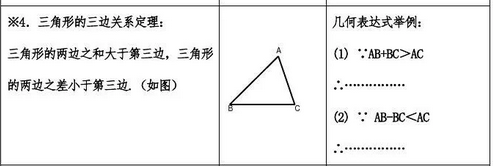
對于任意一個三角形，其任意兩邊之和大于第三邊，任意兩邊之差小于第三邊。用數學表達式表示為：

設三角形的三邊長分別為 a 、b 、c ，則滿足：

1. a + b > c 

2. a + c > b 

3. b + c > a 

同時，任意兩邊之差小于第三邊：

1. |a - b| < c 

2. |a - c| < b 

3. |b - c| < a 

（二）幾何意義：

- 兩邊之和大于第三邊：這是構成三角形的基本條件。如果三條線段不滿足這個條件，就無法構成三角形。

- 兩邊之差小于第三邊：這是兩邊之和大于第三邊的推論，可以理解為第三邊必須大于兩邊之差。

（三）證明思路：

可以通過“兩點之間線段最短”這一公理來證明。例如，在三角形ABC中，點A到點B的直線距離是最短的，因此繞過點C的路徑（即兩邊之和）必然大于直接路徑（第三邊）。

（四）應用：

1. 判斷三條線段能否構成三角形：只需驗證是否滿足上述不等式。

- 例如：邊長為3、4、5的三角形滿足 3+4>5 、3+5>4 、4+5>3 ，可以構成三角形。

- 邊長為1、2、4的線段不滿足 1+2>4 ，無法構成三角形。

2. 求邊長的取值范圍：已知兩邊長度，可以確定第三邊的范圍。

- 例如：已知兩邊長為5和7，則第三邊 x  滿足 7-5 < x < 7+5 ，即 2 < x < 12 。

（五）注意事項：

- 定理適用于所有三角形（銳角、直角、鈍角）。

- 在等邊三角形中，三邊相等，所有不等式均成立（如 a + a > a ）。

總結

三角形三邊關系定理是幾何學中的基礎定理，用于判斷三條線段能否構成三角形，并推導邊長的范圍。掌握該定理有助于解決與三角形邊長相關的問題。

標簽:  三角形 三角形的三邊關系定理