直線與圓心的距離d怎么求?

答：直線與圓心的距離 dd 可以通過以下公式求解：

設直線的方程為 Ax + By + C = 0Ax+By+C=0，圓心的坐標為 (a, b)(a,b)。則直線與圓心的距離 dd 為：

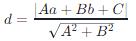
這里：

∣Aa+Bb+C∣ 表示 Aa + Bb + CAa+Bb+C 的絕對值。

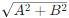是直線的法向量 (A, B)的模。

這個公式是基于點到直線的距離公式推導出來的，適用于任何點至任何直線的距離計算，包括圓心到直線的距離。

舉個例子，如果直線的方程是 3x−4y+5=0，圓心的坐標是 (1, 2)，那么直線與圓心的距離  d 可以計算如下：

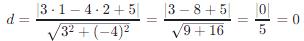
所以，這條直線與圓心的距離是 0，意味著圓心在直線上。

標簽:  直線與圓心的距離d怎么求