三角形垂心是三角形幾何中的一個重要概念，它指的是三角形三條高的交點。在三角形中，從一個頂點向它的對邊（或對邊的延長線）所做的垂線稱為該頂點的高。以下是三角形垂心的定義及其性質：

（一） 定義

三角形的垂心（Orthocenter）是指三角形三條高的交點。這里的高可以是實際的高，也可以是高的延長線。

（二） 性質

1. 交點性質：三角形的垂心是三條高的交點，這三條高分別從三角形的每個頂點垂直于對邊（或其延長線）。

2. 位置關系：

- 在銳角三角形中，垂心位于三角形內部。

- 在直角三角形中，垂心位于直角頂點。

- 在鈍角三角形中，垂心位于三角形外部。

3. 角度關系：垂心到三角形各邊的距離與該邊的對角成正比。

4. 線段長度關系：垂心到三角形各頂點的距離有特定的比例關系，這些關系可以通過三角形的面積和邊長來表示。

5. 中位線性質：垂心、外心和重心三點共線，且重心將垂心與外心的連線分為2:1的比例，即垂心到重心的距離是重心到外心距離的兩倍。

6. 垂心軌跡：在平面直角坐標系中，對于頂點在坐標軸上的三角形，其垂心的軌跡通常是一個圓。

7. 垂心與外心的關系：在任意三角形中，垂心和外心之間的距離  d  滿足以下關系：

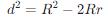
其中  R 是三角形的外接圓半徑， r  是內切圓半徑。

8. 垂心與內心和旁心的關系：垂心、內心和旁心（三角形旁切圓的圓心）共線，這條直線稱為三角形的歐拉線。

了解三角形的垂心及其性質有助于解決一些幾何問題，尤其是在涉及高的計算和三角形的對稱性質時。在解析幾何和三角學中，垂心的概念也經常被使用。

標簽:  三角形垂心的概念及性質