一元二次方程的根指的是能夠使方程成立的未知數的值。換句話說，如果你將這個值代入方程中，方程兩邊的表達式會相等，從而使方程成立。

具體來說，對于一元二次方程 ax^2 + bx + c = 0 ，其中  a ≠0 ，方程的根是滿足以下條件的數  x ：

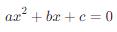
這個方程的根可以是實數也可以是復數，具體取決于判別式 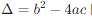的值：

- 如果 △ > 0 ，方程有兩個不相等的實數根。

- 如果 △ = 0 ，方程有兩個相等的實數根（重根）。

- 如果 △ < 0 ，方程沒有實數根，而是有兩個共軛復數根。

一元二次方程的根可以通過求根公式（二次公式）來計算：

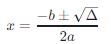
這里的 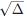是判別式的平方根，± 表示方程有兩個解，一個是加號，一個是減號。

例如，對于方程 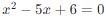，我們可以通過因式分解或者求根公式來找到根：

因式分解： (x - 2)(x - 3) = 0 

所以，根是 x = 2 和 x = 3。這意味著當  x  是 2 或 3 時，方程 x^2 - 5x + 6 = 0 成立。

標簽:  一元二次方程的根