代數(shù)式分為哪幾類?
時間:2025-01-02 14:02:14
最佳答案
代數(shù)式可以分為以下幾類:
1. 單項式:只包含一個項的代數(shù)式。例如:5x^2、3ab、−7。
2. 多項式:由多個單項式通過加法或減法連接而成的代數(shù)式。例如:2x^3 + 4x^2 - 3x + 1、a^2 - b^2。
多項式可以根據(jù)項數(shù)和次數(shù)進一步分類:
- 二項式:包含兩個項的多項式,如 x + 1、a^2 - b^2。
- 三項式:包含三個項的多項式,如 2x^2 - 3x + 1。
- 單項式也可以看作是多項式的特例。
根據(jù)最高項的次數(shù),多項式還可以分為:
- 一元一次多項式:最高次數(shù)為1的多項式,如 3x + 2。
- 一元二次多項式:最高次數(shù)為2的多項式,如 x^2 - 4x + 4。
- 以此類推,還有一元三次多項式、一元四次多項式等。
3. 分式:分子或分母中至少有一個是代數(shù)式的分數(shù)形式的表達式。例如: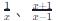 。
。
4. 根式:包含根號的表達式,根號內(nèi)的部分可以是代數(shù)式。例如: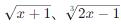 。
。
5. 有理式:可以表示為兩個多項式之比的代數(shù)式,包括分式和可以化為分式的根式。例如: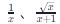 。
。
6. 無理式:不能表示為兩個多項式之比的代數(shù)式,通常是那些無法化為分式的根式。例如: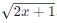 。
。
這些分類是根據(jù)代數(shù)式的結構和組成來劃分的,不同類型的代數(shù)式在運算和性質(zhì)上有各自的特點。
相關推薦