高中數學中關于橢圓的知識點主要包括以下幾個方面：

1. 橢圓的定義：

- 橢圓是平面內到兩個定點（焦點）距離之和為常數的點的軌跡。

- 這個常數大于兩定點之間的距離。

2. 橢圓的標準方程：

- 橢圓中心在原點，長軸在x軸上的標準方程為。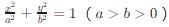

- 橢圓中心在原點，長軸在y軸上的標準方程為 。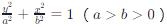

- 其中，a 是半長軸，b是半短軸。

3. 橢圓的幾何性質：

- 焦點：位于長軸上，兩焦點到橢圓上任意一點的距離之和為2a。

- 焦距：兩焦點之間的距離，記為2c，其中 。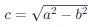

- 準線：與橢圓相應的焦點和離心率有關的直線。

- 離心率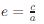：，表示橢圓的扁平程度，0 < e < 1。

4. 橢圓的離心率：

- 離心率 e的計算公式。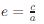

- 離心率反映了橢圓與圓的偏離程度，e越小，橢圓越接近圓。

5. 橢圓的切線與法線：

- 橢圓上任意一點的切線方程。

- 橢圓上任意一點的法線方程。

6. 橢圓的方程變換：

- 如何通過平移、旋轉將橢圓方程轉換為標準形式。

7. 橢圓的面積：

- 橢圓的面積公式為 A=πab。

8. 橢圓與直線的位置關系：

- 直線與橢圓相交、相切或不相交的判定方法。

- 求解直線與橢圓的交點坐標。

9. 橢圓的應用問題：

- 解決實際問題時，如何建立橢圓模型。

這些知識點是高中數學橢圓部分的基礎，掌握這些內容對于解決橢圓相關的題目至關重要。在學習過程中，需要通過大量的練習來熟練運用這些知識點。

標簽:  高中數學 橢圓 知識點