萊布尼茨公式（Leibniz formula）通常指的是數(shù)學(xué)家戈特弗里德·威廉·萊布尼茨發(fā)現(xiàn)的一個(gè)公式，它用于計(jì)算兩個(gè)函數(shù)的乘積的 n 階導(dǎo)數(shù)。這個(gè)公式在數(shù)學(xué)分析中非常重要，尤其是在研究多項(xiàng)式和三角函數(shù)的導(dǎo)數(shù)時(shí)。

萊布尼茨公式表達(dá)如下：

設(shè) f(x) 和 g(x) 是可導(dǎo)函數(shù)，那么它們的乘積 f(x)g(x) 的 n 階導(dǎo)數(shù)可以表示為：

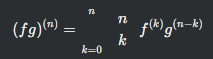
其中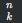，是組合數(shù)，表示從 n 個(gè)不同元素中取出 k 個(gè)元素的組合數(shù)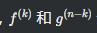，分別是 f 和 g 的 k 階和 (n-k) 階導(dǎo)數(shù)。

萊布尼茨公式說(shuō)明了如何通過(guò)較低階的導(dǎo)數(shù)來(lái)計(jì)算較高階的導(dǎo)數(shù)，它是通過(guò)將兩個(gè)函數(shù)的導(dǎo)數(shù)以各種可能的方式相乘并求和來(lái)得到的。這個(gè)公式在理論和實(shí)際應(yīng)用中都非常有用，比如在求解微分方程、計(jì)算冪級(jí)數(shù)展開等方面。

萊布尼茨公式的一個(gè)特例是二項(xiàng)式定理，當(dāng) f(x) = x 和 g(x) = x 時(shí)，萊布尼茨公式就變成了二項(xiàng)式定理的導(dǎo)數(shù)形式。

標(biāo)簽:  萊布尼茨公式 導(dǎo)數(shù)